Le principe du cashback dans les jeux d’argent

Le cashback, ou remboursement partiel, consiste pour un opérateur à reverser un pourcentage des pertes nettes d’un joueur sur une période donnée. Contrairement au bonus de dépôt classique, il ne s’agit pas d’argent fictif mais d’un crédit réel, souvent versé automatiquement. En France, sous le contrôle de l’ANJ, cette mécanique s’est imposée comme un outil de fidélisation majeur. Lisez la suite sur casino en ligne sécurisé.

Le fonctionnement repose sur une formule simple : montant des pertes moins montant des gains, multiplié par le taux de remboursement. Un joueur qui perd 200 € et gagne 50 € sur une semaine affiche une perte nette de 150 €. Avec un taux de 10 %, il récupère 15 €. Ce calcul évite les abus : seuls les joueurs réellement perdants sont remboursés.

Les taux observés sur le marché français oscillent entre 5 % et 15 %. Les plateformes premium, comme Voglia, appliquent un cashback hebdomadaire pouvant atteindre 15 % sur les pertes nettes, sans plafond artificiel bas. Ce niveau dépasse nettement la moyenne nationale, située autour de 8 %.

Certains programmes distinguent le cashback sur les paris sportifs et sur le casino. Le premier se calcule souvent sur les cotes inférieures à 2,00, le second sur les tours perdants. Cette segmentation permet à l’opérateur de maîtriser son exposition financière tout en récompensant la régularité.

Les différents types de remboursements

Le remboursement prend plusieurs formes. Le cashback fixe s’applique à toutes les mises, indépendamment du résultat. Le cashback progressif augmente selon le volume joué : un joueur atteignant 5 000 € de mises mensuelles peut voir son taux passer de 5 % à 12 %. Le remboursement sur perte, plus rare, ne se déclenche qu’en cas de solde négatif.

Il existe aussi le freebet remboursé : si un pari est perdu, l’opérateur restitue la mise sous forme de crédit de jeu. Cette formule, très répandue sur les paris sportifs, séduit 47 % des joueurs français selon les données sectorielles. Elle diffère du cashback pur, car le crédit doit souvent être rejoué au moins une fois.

Voglia propose un système hybride : 10 % de cashback instantané sur les pertes quotidiennes et 15 % de remboursement hebdomadaire cumulé. Ce double dispositif couvre à la fois les joueurs occasionnels et les profils à forte activité.

Les conditions de retrait varient. Un cashback crédité en argent réel est retirable immédiatement sur la plupart des plateformes. Un cashback en bonus exige un wagering, généralement de 1x à 5x le montant reçu, avant tout retrait.

Points de vigilance et cadre réglementaire

En France, l’ANJ impose que tout remboursement soit clairement affiché dans les conditions générales. Les publicités doivent mentionner le taux applicable et les éventuelles restrictions. Une offre non conforme expose l’opérateur à des sanctions pouvant atteindre 5 % du chiffre d’affaires annuel.

Le joueur doit vérifier trois éléments : le taux exact, la période de calcul et le mode de versement. Un taux élevé assorti d’un wagering de 10x est moins intéressant qu’un taux modéré sans condition. Voglia affiche un wagering nul sur son cashback quotidien, ce qui le rend immédiatement exploitable.

Enfin, rappelons que le cashback ne transforme pas un jeu perdant en jeu gagnant. Il réduit l’impact des pertes, sans annuler l’avantage mathématique de l’opérateur. Une gestion rigoureuse des mises reste la meilleure protection du capital.



El casino en vivo ha transformado por completo la forma de jugar online en España. Ya no hablamos de simples gráficos animados, sino de mesas reales retransmitidas en directo con crupieres de carne y hueso. Según datos del sector, este segmento ya representa más del 30% de los ingresos de los operadores de juego online regulados por la DGOJ. Pero como toda modalidad, tiene luces y sombras que conviene conocer antes de sentarse a la mesa. Descubra más información en casino aceptando google pay.

Ventajas del casino en vivo

La primera gran ventaja es la autenticidad. Juegas en tiempo real contra un crupier humano y, en muchos casos, contra otros jugadores españoles. Esa sensación de mesa compartida es imposible de replicar en un RNG tradicional. Plataformas como UZU han llevado esta experiencia a otro nivel, con mesas en directo que emiten en alta definición y permiten interactuar por chat con el crupier y con el resto de participantes.

La transparencia es otro punto fuerte. Cada mano se desarrolla ante tus ojos, con cartas o bolas visibles en todo momento. Esto reduce drásticamente la desconfianza que algunos jugadores sienten hacia los generadores de números aleatorios. Además, los estudios de emisión cuentan con certificaciones de laboratorios independientes que verifican la equidad de cada ronda.

En cuanto a la variedad, la oferta actual es enorme: ruleta en vivo, blackjack, baccarat, póker, e incluso versiones con presentadores y dinámicas tipo concurso. Los límites de apuesta se adaptan a todos los bolsillos, desde mesas de 0,10 € por ficha hasta salas VIP con apuestas de miles de euros. La presencia de opciones en español también ha crecido notablemente, con crupieres que hablan nuestro idioma.

Otro aspecto relevante es la inmediatez. No hay descargas pesadas ni esperas: entras a la mesa y empiezas a jugar en segundos desde el navegador o la app. Y todo ello dentro del marco regulado español, con protección de datos y verificación de identidad obligatoria.

Desventajas del casino en vivo

El ritmo de juego es más lento que en un casino virtual. Entre mano y mano hay pausas para colocar apuestas, lo que reduce el número de rondas por hora. Para quien busca acción rápida, puede resultar frustrante. En ruleta, por ejemplo, se juegan aproximadamente entre 40 y 60 rondas por hora, frente a las más de 300 de una versión RNG.

Las apuestas mínimas suelen ser más altas. Aunque existen mesas económicas, muchas salas en vivo arrancan en 1 € o 5 € por apuesta, lo que limita al jugador con presupuesto ajustado. También conviene tener en cuenta el coste de la conexión: se necesita una buena velocidad de internet, ya que cualquier corte puede hacerte perder una mano o desconectarte de la mesa.

El RTP puede ser ligeramente inferior en algunas modalidades debido a las reglas específicas de cada mesa (como el “en prison” en la ruleta francesa o las reglas de la carta del crupier en blackjack). Es fundamental leer las condiciones antes de apostar, porque pequeñas variaciones marcan la diferencia a largo plazo.

Por último, la disponibilidad horaria: aunque muchas mesas operan 24/7, las salas con crupieres en español tienen horarios más limitados. Fuera de esas franjas, toca jugar en mesas internacionales en inglés u otros idiomas.

Conclusión: ¿merece la pena el casino en vivo?

Depende de lo que busques. Si valoras la experiencia social, la transparencia y la sensación de estar en un casino real sin salir de casa, las ventajas superan claramente a los inconvenientes. Si prefieres velocidad, apuestas bajas y máxima variedad de slots, el casino virtual sigue siendo más adecuado.

En cualquier caso, juega siempre en operadores con licencia de la DGOJ, establece límites de tiempo y dinero, y recuerda que el casino es entretenimiento, no una fuente de ingresos. La clave está en disfrutar de la experiencia con responsabilidad.



¿Qué es el autojuego y por qué se ha vuelto tan popular?

El autojuego, o giro automático, es una función que permite programar un número determinado de giros en una tragamonedas sin necesidad de pulsar el botón en cada ocasión. Basta con seleccionar la apuesta, fijar la cantidad de tiradas y dejar que el sistema ejecute la secuencia de forma continua. En España, esta modalidad está disponible en la práctica totalidad de los casinos online regulados por la DGOJ, y su uso se ha disparado en los últimos años: se estima que más del 60 % de las sesiones de juego en slots incluyen al menos una ronda de autojuego. Puede encontrar más detalles en casino paypal españa.

La razón principal es la comodidad. No tener que hacer clic constantemente permite mantener un ritmo de juego uniforme, algo que muchos jugadores valoran cuando quieren probar una máquina durante varias decenas de tiradas. Además, ayuda a evitar impulsos puntuales, ya que las decisiones se toman antes de empezar, no en pleno desarrollo de la partida.

No obstante, conviene entender que el autojuego no altera las probabilidades. Cada giro sigue siendo independiente y sujeto al RTP configurado por el desarrollador, que en la mayoría de títulos ronda entre el 94 % y el 97 %. La función solo automatiza la ejecución, no mejora las opciones de premio.

Cómo configurar el autojuego paso a paso

El proceso es sencillo y muy similar entre plataformas. En primer lugar, se elige el importe de la apuesta por línea o por giro. Después se localiza el botón de autojuego, normalmente identificado con un icono de flechas circulares o la palabra «Auto». A continuación se define el número de tiradas, que suele oscilar entre 10 y 100 según el operador.

Muchos sistemas permiten añadir condiciones de parada, un aspecto clave para gestionar el bankroll:

• Detener la secuencia si se alcanza una ganancia determinada.
• Parar cuando el saldo baje de un umbral fijado.
• Interrumpir tras una victoria de cierto importe.
• Cancelar si se activa una ronda de bonificación.

Estas opciones convierten el autojuego en una herramienta de control, no en un piloto automático sin retorno. Un jugador que fija un límite de pérdida de 20 EUR y una ganancia objetivo de 50 EUR está aplicando una estrategia disciplinada que reduce la exposición emocional.

En operadores premium como nuestro casino recomendado, el panel de autojuego incorpora además un contador de tiradas restantes y un resumen de ganancias acumuladas, lo que aporta transparencia total durante la sesión.

Ventajas, límites y buenas prácticas

La principal ventaja es la velocidad y la comodidad, pero también la consistencia: el autojuego elimina pausas accidentales y permite cubrir más tiradas en menos tiempo. Sin embargo, esa misma velocidad puede ser un arma de doble filo, ya que el saldo se consume más rápido si no se han definido límites previos.

La recomendación general es usar secuencias cortas, de entre 20 y 50 giros, y revisar el resultado antes de lanzar otra tanda. Fijar siempre una pérdida máxima y una ganancia objetivo es tan importante como elegir una tragamonedas con un RTP competitivo.

En definitiva, el autojuego es una función cómoda y segura siempre que se use con criterio. Configurar límites, elegir apuestas acordes al presupuesto y aprovechar las condiciones de parada son la mejor forma de disfrutar de las tragamonedas en España con control total.



Elegir un casino online fiable en España no debería ser una cuestión de suerte. La clave está en un detalle que muchos jugadores pasan por alto: la licencia de la Dirección General de Ordenación del Juego (DGOJ). Este organismo público supervisa todas las plataformas que operan legalmente, y su sello garantiza que la casa cumple con requisitos estrictos de seguridad, juego responsable y pago de premios. Puede encontrar más detalles en google pay casino.

En la actualidad, solo un número reducido de operadores cuentan con autorización específica para el mercado español. Esto significa que, de las cientos de webs accesibles desde territorio nacional, únicamente una fracción está sometida a la vigilancia de la DGOJ. Saber identificar esas plataformas marca la diferencia entre jugar con garantías o exponerse a riesgos innecesarios.

Qué comprobar antes de registrarte

El primer paso es verificar el número de licencia en el pie de página del sitio. La DGOJ exige mostrarlo de forma visible, junto al enlace al Registro General de Interdicciones de Acceso al Juego. Si no aparece, conviene desconfiar. Un casino regulado también debe ofrecer información clara sobre depósitos, retiradas y plazos de pago.

Otro aspecto determinante es la variedad de métodos de pago en euros. Las plataformas con licencia aceptan tarjetas, transferencias y monederos electrónicos sin conversiones de divisa, ya que operan exclusivamente en EUR. Además, todas deben integrar sistemas de autoexclusión y límites de depósito, herramientas obligatorias para promover un juego responsable.

La atención al cliente merece un análisis aparte. Un operador serio ofrece soporte en español, con canales como chat en vivo o correo electrónico, y tiempos de respuesta razonables. También es recomendable revisar la política de bonos: los términos y condiciones deben estar redactados en castellano y sin ambigüedades.

Criterios de calidad que marcan la diferencia

Más allá del cumplimiento legal, hay factores que elevan la experiencia. La velocidad de retirada es uno de los más valorados: un casino eficiente procesa los pagos en menos de 24 horas. Asimismo, la presencia de proveedores de software reconocidos garantiza juegos auditados y resultados aleatorios verificables.

Un catálogo amplio, con miles de títulos que abarcan tragaperras, ruleta, blackjack y apuestas deportivas, indica una plataforma bien surtida. También conviene fijarse en la calidad mobile: hoy más del 70% del tráfico en España se genera desde dispositivos móviles, por lo que una app o web optimizada resulta indispensable.

Los incentivos económicos, siempre bajo condiciones razonables, añaden atractivo. Un ejemplo destacado es el de plataformas premium como Spin Mama, que combinan una selección cuidada de juegos con promociones transparentes y un servicio de atención pensado para el jugador español. Este tipo de operadores entienden que la confianza se construye con hechos, no solo con reclamos publicitarios.

Señales de alarma y buenas prácticas

Existen indicios que deben hacerte desconfiar de inmediato: ausencia de licencia DGOJ, bonos con requisitos imposibles de cumplir, retiradas que se retrasan semanas sin justificación o un servicio de atención que no responde en español. Cualquiera de estas señales sugiere que la plataforma no está a la altura de lo que exige el mercado regulado.

Por el contrario, un buen casino con licencia DGOJ se caracteriza por la transparencia en sus términos, la agilidad en los pagos y el compromiso con el juego responsable. Antes de depositar, dedica unos minutos a comparar condiciones, leer opiniones verificadas y comprobar el historial del operador. La información es tu mejor aliada para disfrutar del entretenimiento con total tranquilidad.



El panorama del juego digital en España ha alcanzado un nivel de madurez notable. Según datos recientes de la Dirección General de Ordenación del Juego (DGOJ), el gasto en juego online superó los 1.000 millones de euros anuales, consolidando un mercado donde la competencia entre operadores es feroz. En 2025, los jugadores españoles ya no se conforman con bonos llamativos; exigen licencias verificadas, pagos inmediatos y una experiencia de usuario impecable. Este análisis repasa los criterios que definen a los casinos más recomendados y por qué algunos nombres destacan muy por encima de la media. Puede encontrar más detalles en casino bizum online.

Qué distingue a un casino online recomendado en 2025

La primera variable es la seguridad jurídica. Todos los operadores legales en España deben contar con la licencia correspondiente de la DGOJ, lo que garantiza protección de fondos y resolución de conflictos. No obstante, la excelencia va más allá del sello regulatorio. Los usuarios valoran cada vez más la transparencia en los términos de las promociones y la rapidez en los retiros.

Un estudio del sector indica que el 68% de los jugadores españoles abandona una plataforma si el proceso de retirada tarda más de 24 horas. Por eso, los casinos mejor valorados en 2025 priorizan métodos locales como Bizum, transferencia instantánea y tarjetas, con tiempos de pago que en muchos casos no superan los 5 minutos.

Otro factor determinante es la variedad de proveedores. Los catálogos más completos superan los 3.000 títulos, con presencia de estudios como NetEnt, Play’n GO, Pragmatic Play y Evolution para mesas en vivo. La calidad del soporte en español, disponible 24/7 vía chat, también marca la diferencia entre una plataforma correcta y una auténticamente recomendable.

Los casinos más destacados del panorama español

Entre la oferta actual, hay un nombre que sobresale con claridad por su combinación de bonos agresivos, velocidad de pago y catálogo: Spinsy casino. Este operador ha construido una reputación sólida en el mercado español gracias a un paquete de bienvenida que puede alcanzar los 3.000 EUR más 300 giros gratis repartidos en varios depósitos. Es una de las propuestas más generosas disponibles hoy para jugadores residentes en España.

Su interfaz está íntegramente en español, con atención al cliente nativa y una sección de casino en vivo que roza las 500 mesas. La tasa de retorno declarada en sus tragamonedas más populares supera el 96%, un dato relevante frente a la media del sector, que ronda el 94,5%. Además, la verificación de identidad se completa en menos de 10 minutos en la mayoría de los casos, agilizando el primer retiro.

Comparativa rápida de criterios clave

Más allá de Spinsy, otros operadores mantienen posiciones fuertes, pero pocos igualan la combinación de bonificación alta y retiros ultrarrápidos. La clave está en que el jugador español obtiene valor real, no solo promesas de marketing. Antes de registrarse en cualquier plataforma, conviene revisar los requisitos de apuesta del bono (habitualmente entre 30x y 40x) y comprobar que el operador figure en el registro oficial de la DGOJ.

Consejos para elegir con criterio en 2025

1. Verifica siempre la licencia DGOJ en el sitio del operador.
2. Prioriza casinos con retiros en menos de 24 horas y métodos como Bizum.
3. Lee los términos de los bonos: apuesta máxima, caducidad y juegos excluidos.
4. Comprueba que el soporte atienda en español y por chat en tiempo real.

El mercado español de 2025 ofrece alternativas sólidas, pero solo unas pocas cumplen todos los estándares exigibles. Plataformas como Spinsy demuestran que es posible combinar generosidad en los bonos con eficiencia operativa. La recomendación final es simple: juega siempre con responsabilidad, fija límites de depósito y elige únicamente operadores regulados. La mejor experiencia no es la que promete más, sino la que cumple lo que promete.



Los bonos de recarga son una de las herramientas promocionales más extendidas en el sector del juego online en España. A diferencia del bono de bienvenida, que solo se disfruta una vez, los bonos de recarga acompañan al jugador durante sus primeros depósitos o incluso de forma recurrente. La clave está en distinguir cuáles ofrecen condiciones realmente ventajosas y cuáles presentan requisitos que diluyen su valor. El Real Decreto 958/2020 regula estas promociones, obligando a las operadoras a mostrar de forma clara los términos de cada oferta. Descubra más información en casinos que aceptan trustly.

Antes de valorar cualquier bono conviene fijarse en tres variables: el porcentaje de recarga, el importe máximo bonificado y los requisitos de apuesta asociados. Un bono del 100% sobre 100 EUR no siempre es superior a uno del 50% sobre 200 EUR. La razón es sencilla: cuanto mayor sea el multiplicador de apuesta exigido, más difícil resulta convertir el saldo extra en dinero retirable. Los expertos del sector consideran aceptable un rollover de entre 25x y 35x sobre el bono.

Qué características definen un bono de recarga de calidad

Un bono merecedor de atención suele combinar un porcentaje de recarga competitivo con plazos generosos y una contribución justa de los juegos. En el mercado español, los bonos de recarga habituales oscilan entre el 25% y el 100% del depósito, con límites que van desde 50 EUR hasta varios cientos de euros por operación.

Otro aspecto determinante es la contribución de las tragamonedas al cumplimiento del rollover. En la mayoría de plataformas, las slots aportan el 100%, mientras que los juegos de mesa como la ruleta o el blackjack suelen contribuir con porcentajes que raramente superan el 20%. Para quien prefiera diversificar, conocer este dato evita sorpresas desagradables.

La vigencia del bono también importa. Muchas promociones caducan a los 7 o 14 días, un plazo que puede resultar insuficiente para completar el rollover sin prisas. Los bonos de recarga con ventanas de 30 días ofrecen una experiencia notablemente más relajada.

• Porcentaje de recarga competitivo: del 50% al 100%.
• Rollover razonable: entre 25x y 35x sobre el importe del bono.
• Plazo de caducidad amplio: 30 días o más.
• Contribución del 100% en tragamonedas.
• Límite máximo de apuesta durante el rollover claramente indicado.

Comparativa práctica de bonos de recarga en España

Para ilustrar qué tipo de ofertas merecen realmente la pena, conviene analizar un escenario comparativo estándar. Tomemos tres bonos ficticios pero representativos del mercado español, con condiciones habituales entre las operadoras autorizadas por la DGOJ.

A primera vista, el bono B resulta llamativo por duplicar el depósito, pero su rollover de 40x sobre un plazo de apenas una semana lo convierte en el menos atractivo. El bono A equilibra bien el porcentaje, el multiplicador y el tiempo, mientras que el C premia a quienes depositan cantidades altas con un rollover bajo, aunque el porcentaje sea modesto.

Un dato relevante: según estudios del sector, alrededor del 60% de los jugadores online en España nunca completa los requisitos de apuesta de un bono de recarga. Esto subraya la importancia de leer los términos antes de aceptar cualquier promoción, por atractiva que parezca en su titular.

Errores frecuentes al elegir un bono de recarga

El error más común es guiarse únicamente por el porcentaje anunciado. Un 200% de recarga con rollover de 50x y caducidad de 48 horas es, en la práctica, mucho menos valioso que un 30% con condiciones flexibles. La publicidad tiende a destacar la cifra grande y a minimizar la letra pequeña.

También es habitual ignorar el límite máximo de apuesta durante el rollover. Si se apuesta más de lo permitido, la promoción puede anularse y el saldo bonificado desaparecer. Por eso conviene verificar siempre ese umbral, que suele situarse entre 2 EUR y 5 EUR por tirada.

Por último, muchos jugadores acumulan bonos sin comprobar su compatibilidad. Algunas operadoras no permiten tener dos promociones activas simultáneamente, lo que puede provocar la pérdida del saldo extra. Revisar las condiciones generales antes de activar un bono de recarga es un hábito que marca la diferencia entre aprovechar la oferta o desperdiciarla.



El catálogo de un casino online español se mide, en gran parte, por la calidad de sus proveedores. No basta con acumular miles de títulos: importa quién los firma. Según datos del sector, más del 70% del volumen de apuestas en tragaperras dentro del mercado regulado español se concentra en apenas una decena de estudios, lo que demuestra que la reputación del desarrollador pesa tanto como el propio juego. En España, la labor de la Dirección General de Ordenación del Juego (DGOJ) garantiza que solo operen compañías con licencia, aunque la selección final de software depende de cada plataforma. Puede encontrar más detalles en casino sin licencia.

Qué hace que un proveedor sea referente

Un desarrollador puntero combina tres factores: tecnología certificada, frecuencia de lanzamientos y capacidad de adaptación al jugador español. Los estudios que lideran el mercado publican entre 8 y 15 novedades al mes, frente a las 2 o 3 de los estudios minoritarios. Además, más del 90% de sus títulos incorporan RTP (retorno al jugador) auditados por laboratorios independientes como eCOGRA o BMM Testlabs, un requisito imprescindible para operar legalmente en España.

La variedad también importa. Los grandes proveedores cubren tragaperras, ruleta en vivo, blackjack, vídeo bingo y juegos con crupier real. Esta amplitud permite que un operador construya una experiencia completa sin depender de terceros menores, lo que se traduce en mayor estabilidad técnica y tiempos de carga más cortos.

Otro criterio decisivo es la localización. Los proveedores que realmente apuestan por el mercado español traducen sus interfaces al castellano, adaptan los límites de apuesta al euro y respetan las restricciones publicitarias vigentes. Esa cercanía se nota en la experiencia diaria del jugador.

Los estudios que dominan el panorama español

Entre los nombres más consolidados destacan NetEnt, Play’n GO, Pragmatic Play, Microgaming y Red Tiger. NetEnt, por ejemplo, mantiene títulos clásicos como Starburst con un RTP del 96,1%, mientras que Pragmatic Play ha logrado colocar más de 300 juegos en operadores españoles. Play’n GO, por su parte, es responsable de sagas como Book of Dead, presente en prácticamente todos los casinos regulados del país.

En el segmento de casino en vivo, Evolution domina con una cuota que supera el 60% del mercado europeo de crupier real. Sus mesas en directo, con dealers formados y emisiones en alta definición, se han convertido en el estándar del sector. No es casualidad que los operadores que integran estos proveedores registren tasas de retención de jugadores hasta un 25% superiores a las de plataformas con catálogos más débiles.

La presencia de proveedores punteros también influye en las bonificaciones. Muchos casinos españoles reservan sus tiradas gratis y promociones para tragamonedas de estudios concretos, ya que conocen su rendimiento y su capacidad de atraer tráfico.

Cómo elegir un casino con buen software

Antes de registrarse, conviene revisar la lista de proveedores que aparece en la web del operador. Un catálogo firmado por al menos ocho o diez estudios reconocidos suele indicar una plataforma sólida y bien integrada. También es útil comprobar la licencia de la DGOJ, que garantiza que los juegos han superado las auditorías exigidas en España.

Otro consejo práctico: fíjate en la sección de juegos nuevos. Los casinos que actualizan su catálogo semanalmente demuestran una relación activa con los proveedores, lo que se traduce en más variedad y mejores condiciones. Un catálogo estancado, en cambio, suele ser señal de integraciones deficientes o acuerdos caducados.

Por último, valora la experiencia en móvil. Los proveedores punteros optimizan sus títulos para HTML5, lo que permite jugar sin descargas y con un rendimiento fluido en cualquier dispositivo. En un mercado donde más del 65% del tráfico ya proviene de smartphones, ese detalle marca la diferencia entre una plataforma ágil y otra que se queda atrás.



El bono de bienvenida es la primera impresión que un casino online ofrece a sus nuevos usuarios, y también el reclamo más repetido en publicidad. Sin embargo, no todos los bonos valen lo que prometen. En España, el sector del juego online movió más de 1.200 millones de euros en ingresos brutos durante el último ejercicio registrado por la Dirección General de Ordenación del Juego, y la competencia por captar jugadores ha convertido las promociones de bienvenida en un campo minado de letra pequeña. Aprender a compararlas con criterio es la diferencia entre aprovechar una ventaja real y quedar atrapado en requisitos imposibles de cumplir. Puede encontrar más detalles en casino crypto seguro.

Los elementos que definen un bono de bienvenida competitivo

Comparar bonos exige mirar más allá de la cifra grande del anuncio. Un “100% hasta 200 €” puede ser excelente o mediocre según las condiciones que lo acompañan. El primer factor es el porcentaje de coincidencia: indica cuánto se iguala tu primer depósito. El segundo es el importe máximo, que limita la bonificación real. Y el tercero, el más decisivo, son los requisitos de apuesta o wagering, expresados como múltiplo (x30, x40, x50). Cuanto más alto, más difícil será convertir el bono en dinero retirable.

La media del mercado español se sitúa en torno a x35 sobre el importe del bono, aunque algunas plataformas lo aplican también sobre el depósito, lo que dispara la exigencia real. Un bono de 100 € con wagering x35 sobre bono requiere apostar 3.500 €; si el requisito se calcula sobre depósito más bono, la cifra sube a 7.000 €. Esa diferencia cambia por completo la ecuación.

Otros factores relevantes incluyen el plazo para completar los requisitos (habitualmente 30 días), las restricciones por juego (las tragaperras suelen aportar el 100% al cómputo, mientras que la ruleta o el blackjack aportan entre el 10% y el 20%), la apuesta máxima permitida durante la promoción y la contribución de cada título al progreso del bono.

Comparativa práctica: qué mirar antes de aceptar una oferta

Una comparación útil ordena los bonos por valor real esperado, no por titular. La siguiente tabla resume los criterios que conviene revisar uno a uno:

También conviene distinguir entre bonos de depósito y bonos sin depósito. Los primeros igualan tu ingreso y suelen alcanzar los 100-200 €; los segundos regalan una cantidad pequeña (5-20 €) pero permiten probar la plataforma sin riesgo. En ambos casos, la operadora debe estar licenciada por la DGOJ y mostrar el número de registro en su web.

Un ejemplo de transparencia en este sentido lo encontramos en plataformas que publican el detalle del wagering en la propia ficha del bono, sin obligar al usuario a bucear en términos y condiciones de veinte párrafos. Ese nivel de claridad es ya un indicador de seriedad.

Errores frecuentes al valorar promociones de bienvenida

El error más común es fijarse solo en el importe máximo. Un bono de 500 € con wagering x50 sobre depósito más bono equivale a apostar 50.000 € antes de retirar nada, cifra inalcanzable para la mayoría de jugadores. En cambio, un bono de 100 € con x25 sobre bono exige solo 2.500 € en apuestas, una meta realista en pocas semanas.

El segundo error es ignorar las restricciones temporales. Si tardas más de lo permitido en completar el wagering, pierdes el bono y las ganancias asociadas. El tercero es no comprobar si las tiradas gratuitas incluidas tienen sus propias condiciones: muchas veces las ganancias de los giros van a un saldo separado con requisitos adicionales.

Por último, conviene verificar la reputación de la operadora mediante reseñas de usuarios reales y foros especializados. Un bono generoso en una plataforma con quejas recurrentes sobre pagos lentos vale menos que uno modesto en un casino que procesa retiradas en menos de 24 horas. La comparación inteligente cruza siempre tres variables: valor económico, condiciones de conversión y fiabilidad de la casa.

En definitiva, elegir bien un bono de bienvenida no consiste en buscar el número más grande, sino en calcular el coste real de convertirlo en dinero. Leer el wagering, comprobar el plazo, revisar la contribución de los juegos y confirmar la licencia española son pasos sencillos que marcan una diferencia enorme en la experiencia final.

Definition:

Equivalent fluid pressure is a simplification of backfill earth pressure against retaining structures. If the backfill behind a cantilever retaining wall or restrained (basement) wall is level, we can use the equivalent pressure. For a cantilever retaining wall, level & drained condition (subdrain), the equivalent fluid pressure is simply the product of Ka * Gamma, where Ka is the Active earth pressure coefficient & Gamma is the moist unit weight of the backfill. For a restrained retaining wall, level & drained condition (subdrain), the equivalent fluid pressure is simply the product of Ko * Gamma, where Ko is the At Rest earth pressure coefficient & Gamma is the moist unit weight of the backfill.

History:

The first mention of the equivalent fluid pressure is in the 1953 publication, “American Association of State Highway Officials, Standard Specifications for Highway Bridges”, currently known as AASHTO Specifications. It said “Structures designed to retain fills should be proportioned to withstand pressure as given by Rankine’s formula; provided, however, that no structures should be designed for less than an equivalent fluid pressure of 30 lb per cu ft”.

Prior discouragement of the EFP method:

Professor Whitney Clark Huntington in his publication, “Earth Pressures and Retaining Walls”, said “The equivalent fluid method is commonly misused by applying it to walls which retain earth with a sloping ground surface..”. This statement was made in 1957, approx. 60 years ago. However, we still see the use of EFP method in today’s retaining wall designs.

Why is EFP not applicable to ascending slopes?

1. The EFP is increased arbitrarily to account for the ascending slope backfill angle while the vertical earth pressure component is sometimes not accounted for in design
2. The direction of the static earth pressure is level but in reality should be parallel to the ascending slope when using the Rankine’s method
3. The direction of the static earth pressure is level but in reality should be same as the soil-wall friction angle in Coulomb’s method
4. The sliding factor of safety computed by EFP will be larger than that calculated from Rankine, Coulomb or Muller-Breslau method (unconservative).
5. The overturning factor of safety computed by EFP will be smaller than that calculated from Rankine, Coulomb or Muller-Breslau method (overly conservative).
6. The Toe bearing pressure will be smaller with EFP method as compared to Rankine, Coulomb or Muller-Breslau method (under-predict induced wall settlement)
7. The Heel bearing pressure will show higher value with the EFP method as compared to Rankine, Coulomb or Muller-Breslau method (in reality eccentricity >B/6)
8. The Moment Demand, Mu, will be slightly larger with the EFP method as compared to Rankine, Coulomb or Muller-Breslau method (extra stem steel required)
9. The top of wall deflection will be slightly larger with the EFP method as compared to Rankine, Coulomb or Muller-Breslau method

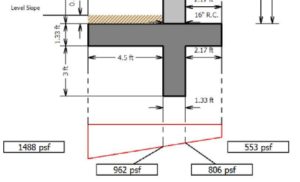 Bearing Press.(EFP method)  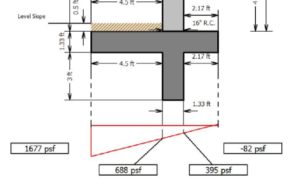                Bearing Press.(Phi/C /Gamma method)

Conclusion:

Geotechnical engineers should start to offer Phi, C, and Gamma values for cantilever and restrained retaining wall design & Wall designers should learn how to compute Active Ka, At Rest Ko, Passive resistance Kp, and Sliding friction coefficient. Professor Huntington discouraged it 70 years ago and SoilStructure Software discourages its use today. EFP is still in v3 of the SoilStructure Retaining Wall software as we hope this is a transitional time from EFP to Phi/C/Gamma.